Интересно знать

Петропавловский собор
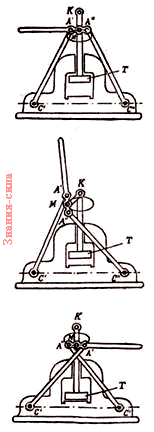
Схема действия пресса, сконструированного П.Л. Чебышевым.
Несмотря на простоту устройства, этот пресс способен создавать огромное давление.
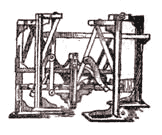
Переступающая машина Чебышева
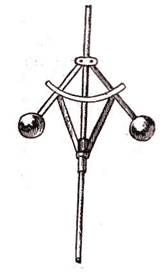
Центробежный регулятор

Петропавловский собор

Схема действия пресса, сконструированного П.Л. Чебышевым.
Несмотря на простоту устройства, этот пресс способен создавать огромное давление.

Переступающая машина Чебышева

Центробежный регулятор
© сайт "Знания-сила".
Читайте начало, часть 1
Многим обогатил механику замечательный мостостроитель Дмитрий Иванович Журавский (1821-1891).
Опыт предшественников — создателей мостов обычного назначения — мало годился для проектирования железнодорожных мостов, которые должны были выносить значительно большие динамические нагрузки.
Опыт строителей, возводивших железнодорожные мосты в разных странах, также немногому мог научить талантливого русского инженера. Известные в ту пору мосты, составленные из ферм системы инженера Гау, не обладали надежной прочностью. Видный инженер строил мостовые фермы, элементы которых были совершенно одинаковы по всей длине, как близ опор, так и в средней части.
Журавский подверг тщательному исследованию ферму Гау. Построив модель её, русский инженер заменил в ней болтовые соединения проволоками. Нагрузив модель и заставляя скрепляющие ферму проволоки колебаться, как струны, он обнаружил, что они в разных частях фермы издают звуки разных тонов. Предвидения Журавского оправдались: нагрузка в разных частях фермы оказалась неодинаковой. Так изящным опытом Журавский установил серьезный недостаток мостов конструкций инженера Гау. Исследование его ошибки послужило Журавскому отправной точкой для создания научно обоснованных методов мостостроения.
Журавский разработал способ расчёта мостовых ферм и, пользуясь своей теорией, спроектировал и построил много замечательных железнодорожных мостов — через Мсту, Цну и другие реки.
Способности Журавского к научному осмысливанию задач строительной практики ярко проявились и тогда, когда ему пришлось заняться проектированием и постройкой металлического шпиля для собора Петропавловской крепости. (В 1857-1858 гг. производилась перестройка шпиля на соборе Петропавловской крепости с заменой деревянных конструкций металлическими).
Взявшись за постройку пирамидального шпиля — такую задачу приходилось решать в мировой технике впервые, — Журавский поставил целью прежде всего подробнейшим образом выяснить характер напряжений, которым подвергнутся элементы будущего сооружения.
Опыты над моделями и математические расчёты, которые Журавский производил во время конструирования шпиля, позволили открыть очень важные для техники методы расчёта двутавровых балок. Такие балки — необходимый элемент мостов, перекрытий зданий, железных каркасов заводских цехов — словом, всякого крупного сооружения.
Тогда же Журавским была разработана и общая теория проектирования сквозных пирамидальных сооружений. Эта теория помогает в наши дни строителям гигантских антенн радиостанций, могучих подъемных кранов, мачт высоковольтных электрических передач.
Последователь Журавского, Николай Аполлонович Белелюбский был инициатором широкого применения в железнодорожном строительстве научных методов испытания материалов, для чего он создал специальную лабораторию, равной которой не было за границей.
Огромное наследство оставил в механике Пафнутий Львович Чебышев (1821-1894). Великий теоретик, прославивший себя блестящими открытиями в математике, с увлечением решал насущные задачи промышленной практики. Чебышев бывал на заводах и фабриках, он с интересом выслушивал суждения инженеров о не поддающихся разрешению технических вопросах и нередко предлагал как математик блестящий выход из затруднения.
Вот один пример. Инженеры-машиностроители были недовольны выпрямляющим механизмом Уатта, так называемым параллелограммом Уатта. Механизм этот, предназначенный для превращения кругового движения в прямолинейное, выполнял свою задачу неудовлетворительно. Движение только в грубом приближении можно было считать прямолинейным. А из-за такого несовершенства параллелограмма Уатта в машинах возникали вредные сопротивления.
На помощь инженерам пришёл Чебышев. Появился метод теоретического расчета выпрямляющих механизмов, то есть механизмов, способных «выпрямлять» вращательное движение, превращать его в прямолинейное. В наши дни подобные механизмы стали основой многих совершенных конструкций.
Работа над выпрямляющим механизмом была для Чебышева отправной точкой в его деятельности по созданию теории механизмов и машин.
Стремясь полнее показать силу механики, Чебышев сам становится инженером. Он создает разнообразнейшие механизмы, способные точно воспроизводить сложные движения, работать с остановками, превращать непрерывное движение в движение прерывистое. Свыше сорока механизмов и восьмидесяти их видоизменений спроектировал ученый. Он строит свою знаменитую переступающую машину, точно воспроизводящую движения идущего животного. Создает гребной механизм, повторяющий сложное движение вёсел лодки, самокатное кресло, модель новой сортировальной машины.
Чебышев изобрёл и автомат для вычислений. Созданный в 1881 году, этот автомат явился как бы продолжением его работы над совершенствованием оригинальной суммирующей машины, изобретенной им тремя годами раньше.
Здесь уместно указать, что арифмометр построен в 1874 году петербургским изобретателем В. Т. Однером. Это прототип арифмометров, которыми пользовались почти сто лет.
В отличие от других счетная машина Чебышева могли работать в быстром темпе, превышающем 500 вычислений в час.
Счетная машина Чебышева не смогла найти себе применения в царской России, и единственный экземпляр её, построенный самим изобретателем, попал во Францию, в Париж, в Музей искусств и ремесел. В отделении технических наук РАН и в Петербургском государственном университете бережно хранятся многие из созданных Чебышевым механизмов. Механизмы Чебышева в действии вызывают восхищение даже у самых искушенных в технике людей.
Инженеры и учёные всего мира черпают в трудах Чебышева методы, формулы, идеи. Когда нужно узнать, при каких условиях проектируемая система рычагов, шарниров, колес может стать цельным механизмом, обращаются к знаменитой структурной формуле Чебышева. Это одна из необходимейших формул для инженеров.
Важным достижением русского учёного было и доказательство знаменитой теоремы трехшарнирных четырехзвенников, описывающих одну и ту же шатунную кривую. Эта теорема была независимо от Робертса три года спустя доказана Чебышевым.
Идеи Чебышева получили развитие в работах его учеников. Перу ученика Чебышева — Александра Михайловича Ляпунова (1857-1918), гениального математика и механика, принадлежит теория устойчивости движения.
Всякая система, механическая или электрическая, во время работы испытывает ряд внешних и внутренних воздействий. Зачастую эти воздействия нарушают согласованность работы отдельных частей системы. Она при этом теряет устойчивость движения, «разлаживается». Возникают вредные вибрации, толчки, усилия.
Теория Ляпунова, рассматривающая условия устойчивости движения, стала основой научного проектирования самых разнообразных машин и устройств. Вся ценность этой теории выявилась лишь в наши дни, дни техники больших скоростей, реактивной авиации, автоматики, телемеханики, радиотехники. Конструкторы сложнейших механических и электрических устройств обязательно проверяют методом, созданным Ляпуновым, будет ли устойчива, надежна в работе создаваемая ими система.
Новую теорию пространственных зубчатых механизмов создал другой ученик Чебышева — X.И. Гохман. Над теорией структуры плоских и пространственных механизмов успешно работал П.И. Сомов.
Во второй половине XIX века, когда в промышленности все шире и шире стали распространяться паровые двигатели, перед инженерами встал вопрос о создании надежно работающих регуляторов, способных точно и безотказно реагировать на малейшее изменение нагрузки на паровую машину. Выдающийся русский механик Иван Алексеевич Вышнеградский (1831 — 1895) положил начало теории автоматического регулирования. Этот труд явился ответом русского ученого на настоятельные требования инженерной практики.
Как нужно регулировать работу паровых машин, было известно уже с давних пор. Их снабжали центробежным регулятором, известным чуть ли не со средних веков и применявшимся еще для регулирован ветряных мельниц. При уменьшении нагрузки на маховик машины этот регулятор сокращал доступ пара в цилиндр, уменьшая тем мощность машины. При возрастании нагрузки регулятор шире открывал паропровод. Принцип, лежащий в основе конструкции этого регулятора, был вполне удовлетворительным. Беда заключалась в том, что рассчитывать заранее центробежный регулятор инженеры не умели. При постройке паровой машины каждый раз приходилось кустарно, путем многочисленных проб, подбирать конструктивные размеры частей регулятора. От тщательности такого «регулирования самого регулятора» и зависела успешная работа новой машины. Неоднократные попытки создать методы предварительного расчета регулятора не давали результатов.
Вышнеградскому удалось решить эту важнейшую научную и техническую задачу. В отличие от своих многочисленных предшественников он рассматривал движение регулятора не изолированно, а во взаимодействии с движением самой машины. Он вывел ряд математических уравнений и, блестяще их проанализировав, создал знаменитые «неравенства Вышнеградского».
Выводы русского учёного имели первостепенное значение для практики. «Неравенства» и построения на их основе «диаграммы Вышнеградского» стали основой расчета чувствительных, безотказно работающих регуляторов. Работа Вышнеградского «О регуляторах прямого действия» была сразу же переведена на несколько иностранных языков.
С развитием техники значение работы Вышнеградского раскрывалось всё шире и шире. Все позднейшие изыскания в области автоматического регулирования, как на незыблемый фундамент, опирались на эту работу русского учёного.
↻Назад ➤ Читайте дальше: Первые русские научно-инженерные достижения (часть 3)
Регулировки чтения: ↵ что это ?
Чтение голосом будет работать во всех современных Десктопных браузерах.
Поделиться в соцсетях: